Подпакет Combinatorica задает определение ряда
Пример 11.5.
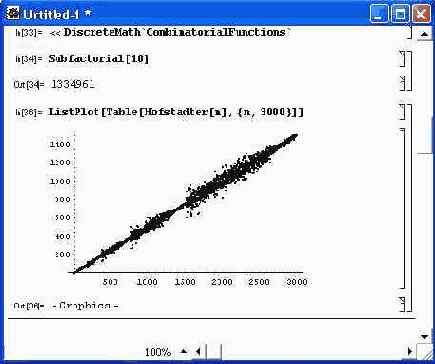
Примеры работы с подпакетом функций комбинаторики
Подпакет Combinatorica задает определение ряда функций комбинаторики и теории графов. Ниже представлены имена функций комбинаторики.
|
Функции перестановок и сочетаний
|
|
|
Backtrack
|
BinarySearch
|
|
Binary Subsets
|
DerangementQ
|
|
Derangements
|
Distinct Permutations
|
|
EquivalenceClasses
|
EquivalenceRelationQ
|
|
Equivalences
|
Eulerian
|
|
FromCycles
|
FromlnversionVector
|
|
GrayCode
|
HeapSort
|
|
Heapify
|
HideCycles
|
|
Index
|
InversePermutation
|
|
Inversions
|
InvolutionQ
|
|
Josephus
|
Ksubsets
|
|
Lexicographic Permutations
|
LexicographicSubsets
|
|
MinimumChangePermutations
|
MultiplicationTable
|
|
NextKSubset
|
Next Permutation
|
|
NextSubset
|
NthPermutation
|
|
NthSubset
|
NumberOf Derangements
|
|
NumberOf Involutions
|
NumberOf Permu tat ion sByCycles
|
|
PermutationGroupQ
|
PermutationQ
|
|
Permute
|
Polya
|
|
RandomHeap
|
RandomKSubset
|
|
RandomPermutation
|
RandomPermutationl
|
|
RandomPermutation2
|
RandomSubset
|
|
RankPermutation
|
RankSubset
|
|
RevealCycles
|
Runs
|
|
SamenessRelation
|
SelectionSort
|
|
SignaturePermutation
|
StirlingFirst
|
|
StirlingSecond
|
Strings
|
|
Subsets
|
ToCycles
|
|
ToInversionVector
|
TransitiveQ
|
<<DiscreteMath`Combinatorica`
?Permute
Permute[l, p] permutes list 1 according to permutation p.
?KSubsets
KSubsets[l, k] gives all subsets of set 1 containing exactly k
elements, ordered lexicographically.
KSubsets[{l, 2, 3, 4, 5}, 2]
{{1, 2}, {1, 3), {1, 4}, {1, 5}, {2, 3), {2, 4}, {2, 5}, {3, 4}, {3, 5}, (4, 5}}
<< DiscreteMath`Combinatorica`
MinimumChangePermutations[{1,2,3}]
{{1, 2, 3}, {2, 1, 3}, {3, 1, 2}, {1, 3, 2}, {2, 3, 1}, {3, 2, 1}}
Map[RankPermutation, Permutations[{1,2,3,4}]]
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23}
InversePermutation[{4,8,5,2,1,3,7,6}]
(5, 4, 6, 1, 3, 8, 7, 2}
Polya[Table[ RotateRight[Range[8],i], {i,8}], m]
1/8 (4m+2m2 +m4 +m8)
Table[NthSubset[n,a,b,c,d], {n,0,15}]
{{}, {a}, {b}, {a, b}, {c}, {a, c}, {b, c}, {a, b, c}, {d}, (a, d}, {b, d}, {a, b, d}, {c, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}
Вторая группа функций комбинаторики представлена следующими функциями.
|
Функции разделения, композиции
и картин Янга
|
|
|
CatalanNumber
|
Compositions
|
|
ConstructTableau
|
DeleteFromTableau
|
|
DurfeeSquare
|
EncroachingListSet
|
|
FerrersDiagram
|
FirstLexicographicTableau
|
|
. Insert IntoTableau
|
LastLexicographicTableau
|
|
Longest IncreasingSubsequence
|
NextComposition
|
|
Next Part it ion
|
NextTableau
|
|
NumberOf Compos it ions
|
NumberOf Partitions
|
|
NumberOf Tableaux
|
PartitionQ
|
|
Partitions
|
RandomComposition
|
|
RandomPartition
|
RandomTableau
|
|
TableauClasses
|
TableauQ
|
|
TableauxToPermutation
|
Tableaux
|
|
TransposePartition
|
TransposeTableau
|
